Gringarten and Ramey Solution for Fractured Aquifers with a Single Horizontal Plane Fracture

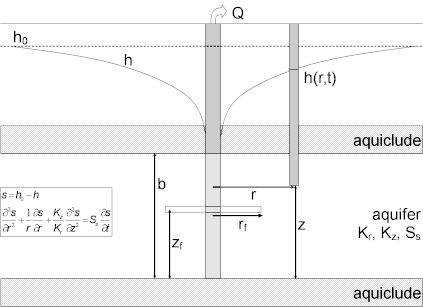
A mathematical solution by Gringarten and Ramey (1974) is useful for determining the hydraulic properties (hydraulic conductivity, specific storage, hydraulic conductivity anisotropy and fracture radius) of fractured aquifers with a single horizontal plane fracture intersecting the control well. Analysis involves matching the solution to drawdown data collected during a pumping test. The solution estimates hydraulic conductivity anisotropy in a vertical (x-z) plane.

You are not restricted to constant-rate tests with the Gringarten and Ramey solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

The early-time response of a pumped well intersecting a horizontal fracture has a distinct signature that you can diagnose with a linear flow plot.

Assumptions

• aquifer has infinite areal extent
• aquifer has uniform thickness
• aquifer potentiometric surface is initially horizontal
• fractured aquifer represented by anisotropic nonleaky confined system with a single plane horizontal fracture
• flow is unsteady
• water is released instantaneously from storage with decline of hydraulic head
• diameter of control well is very small so that storage in the well can be neglected

Equations

The following equation by Gringarten and Ramey (1974) predicts drawdown at a fixed point (piezometer) in an anisotropic confined aquifer with a uniform-flux horizontal fracture:

$$s=\frac{Q}{4\pi \sqrt{K_r{K}_z}{r}_f}\frac{2}{H_D}{\int }_0^{t_D}P·Z\frac{d\tau }{\tau }\text{(1)}$$ $$P=e^{-\frac{r_D^2}{4\tau }}{\int }_0^1{I}_0\left(\frac{r_D\upsilon }{2\tau }\right)e^{-\frac{{\upsilon }^2}{4\tau }}\upsilon d\upsilon \text{(2)}$$ $$Z=1+2\sum _{n=1}^{\infty }{e}^{-\frac{n^2{\Pi }^2\tau }{H_D^2}}\cos \left(n\pi \frac{z_f}{b}\right)\cos \left(n\pi \frac{z}{b}\right)\text{(3)}$$ $$H_D=\frac{b}{r_f}\sqrt{\frac{K_r}{K_z}}\text{(4)}$$ $$r_D=r/r_f\text{(5)}$$ $$t_D=\frac{K_{r}t}{S_s{r}_f^2}\text{(6)}$$

where

• $b$ is aquifer saturated thickness [L]
• $I_0$ is modified Bessel function of first kind, zero order
• $K_r$ is radial hydraulic conductivity [L/T]
• $K_z$ is vertical hydraulic conductivity [L/T]
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $r_f$ is radius of horizontal fracture [L]
• $s$ is drawdown [L]
• $S_s$ is specific storage [L^-1]
• $t$ is elapsed time since start of pumping [T]
• $\tau$ and $\upsilon$ are variables of integration
• $z$ is distance in z direction [L]

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• saturated thickness
• radius and depth of horizontal fracture

Solution Options

• variable pumping rates
• multiple pumping wells
• multiple observation wells
• boundaries

Estimated Parameters

• $K_r$ (radial hydraulic conductivity)
• $S_s$ (specific storage)
• $K_z/K_r$ (hydraulic conductivity anisotropy ratio)
• $R_f$ (radius of fracture)

Curve Matching Tips

• Use linear flow plots to help diagnose linear flow.
• Match the Cooper and Jacob (1946) solution to late-time data to obtain preliminary estimates of aquifer properties.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $K_z/K_r$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

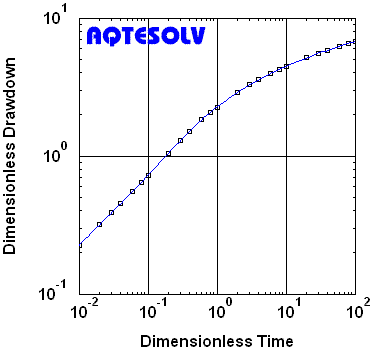
Benchmark

References

Gringarten, A.C. and H.J. Ramey, 1974. Unsteady state pressure distributions created by a well with a single horizontal fracture, partial penetration or restricted entry, SPE Journal, pp. 413-426.