Theis Solution for Nonleaky Confined Aquifers

Charles Vernon Theis (1900-1987) was the first hydrologist to develop a rigorous mathematical model of transient flow of water to a pumping well by recognizing the physical analogy between heat flow in solids and groundwater flow in porous media.

The Theis (1935) solution (or Theis nonequilibrium method) introduced a groundbreaking tool for determining the hydraulic properties (transmissivity and storativity) of nonleaky confined aquifers. Analysis with the Theis method is performed by matching the Theis type curve to drawdown data plotted as a function of time on double logarithmic axes.

Subsequent work by Hantush (1961a; 1961b; 1964) extended the Theis method to correct for partially penetrating wells. When you choose the Theis solution in AQTESOLV, you may analyze data from both fully and partially penetrating wells.

You are not restricted to constant-rate tests with the Theis solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

Assumptions

• aquifer has infinite areal extent
• aquifer is homogeneous and of uniform thickness
• control well is fully or partially penetrating
• flow to control well is horizontal when control well is fully penetrating
• aquifer is nonleaky confined
• flow is unsteady
• water is released instantaneously from storage with decline of hydraulic head
• diameter of a pumping well is very small so that storage in the well can be neglected

Equations

The Theis equation for flow to a fully penetrating line sink discharging at a constant rate in a homogeneous, isotropic and nonleaky confined aquifer of infinite extent is as follows:

$$s=\frac{Q}{4\pi T}{\int }_{\text{u}}^{\infty }\frac{{\text{e}}^{\mathit{-y}}}{y}\mathrm{d}y\text{(1)}$$ $$u=\frac{r^{2}S}{4Tt}\text{(2)}$$

Groundwater hydrologists commonly refer to the integral in (1) as the Theis well function, abbreviated as $\text{w}\left(u\right)$. Therefore, we may write the Theis equation in compact notation as follows:

$$s=\frac{Q}{4\pi T}\mathrm{w}\text{(}u\text{)}\text{(3)}$$ $$\mathrm{w(}u\mathrm{)}=-0.5772-\mathrm{ln(}u\text{)}+u-\frac{u^2}{2·2!}+\frac{u^3}{3·3!}-\frac{u^4}{4·4!}+···\text{(4)}$$

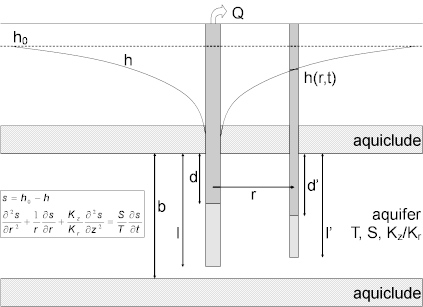
A partially penetrating pumping well produces vertical components of flow in the aquifer. Hantush (1961a, b; 1964) derived equations extending the Theis method to include partial penetration effects in nonleaky confined aquifers. In the case of a piezometer, the following equation applies:

$$s=\frac{Q}{4\pi T}[\mathrm{w}\left(u\right)+\frac{2b}{\pi \left(l-d\right)}\sum _{n=1}^{\infty }\frac{1}{n}(\sin \left(\frac{n\pi l}{b}\right)-\sin \left(\frac{n\pi d}{b}\right))·\cos \left(\frac{n\pi z}{b}\right)·\mathrm{w}\left(u\mathrm{,}\beta \right)]\text{(5)}$$ $$\beta =\sqrt{K_z/K_r}\frac{n\pi r}{b}\text{(6)}$$

The following equation computes drawdown for a partially penetrating observation well:

$$s=\frac{Q}{4\pi T}[\mathrm{w}\left(u\right)+\frac{2b^2}{{\pi }^2\left(l-d\right)\left(l^{\prime }-d^{\prime }\right)}\sum _{n=1}^{\infty }\frac{1}{n^2}\left(\sin \left(\frac{n\pi l}{b}\right)-\sin \left(\frac{n\pi d}{b}\right)\right)·\left(\sin \left(\frac{n\pi l^{\prime }}{b}\right)-\sin \left(\frac{n{\pi d}^{\prime }}{b}\right)\right)·\mathrm{w}\left(u\mathrm{,}\beta \right)]\text{(7)}$$

where

• $b$ is aquifer thickness [L]
• $d$ is the depth to the top of pumping well screen [L]
• $d^{\prime }$ is the depth to the top of observation well screen [L]
• $K_r$ is the radial (horizontal) hydraulic conductivity [L/T]
• $K_z$ is the vertical hydraulic conductivity [L/T]
• $l$ is the depth to the bottom of pumping well screen [L]
• $l^{\prime }$ is the depth to the bottom of observation well screen [L]
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $s$ is drawdown [L]
• $S$ is storativity [dimensionless]
• $t$ is elapsed time since start of pumping [T]
• $T$ is transmissivity [L²/T]
• $\text{w}\left(u\right)$ is the Theis well function for nonleaky confined aquifers [dimensionless]
• $\text{w}(u,\beta )$ is the Hantush and Jacob well function for leaky confined aquifers [dimensionless]
• $y$ is a variable of integration
• $z$ is piezometer depth [L]

At large distances, the effect of partial penetration becomes negligible when

$$r>1.5b/\sqrt{K_z/K_r}\text{(8)}$$

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• partial penetration depths (optional)
• saturated thickness (for partially penetrating wells)
• hydraulic conductivity anisotropy ratio (for partially penetrating wells)

Solution Options

• variable pumping rates
• multiple pumping wells
• multiple observation wells
• partially penetrating pumping and observation wells
• boundaries

Estimated Parameters

AQTESOLV provides visual and automatic methods for matching the Theis nonequilibrium method to data from pumping tests and recovery tests. The estimated aquifer properties are as follows:

• $T$ (transmissivity)
• $S$ (storativity)
• $K_z/K_r$ (hydraulic conductivity anisotropy ratio)
• $b$ (saturated aquifer thickness)

Partially penetrating wells are required to estimate $K_z/K_r$ and $b$.

Curve Matching Tips

• Use the Cooper and Jacob (1946) solution to obtain preliminary estimates of aquifer properties.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• For partially penetrating wells, select values of $K_z/K_r$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

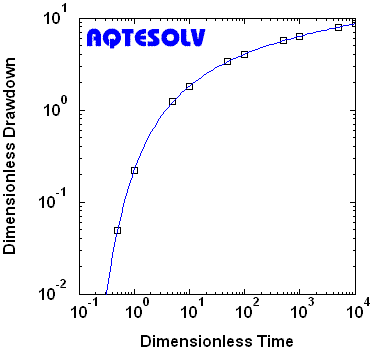
Benchmark

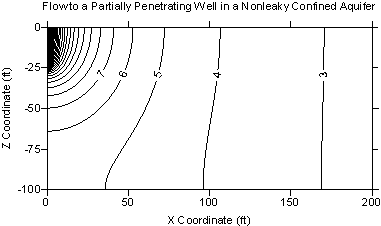
Example

References

Theis, C.V., 1935. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage, Am. Geophys. Union Trans., vol. 16, pp. 519-524.

Hantush, M.S., 1961a. Drawdown around a partially penetrating well, Jour. of the Hyd. Div., Proc. of the Am. Soc. of Civil Eng., vol. 87, no. HY4, pp. 83-98.

Hantush, M.S., 1961b. Aquifer tests on partially penetrating wells, Jour. of the Hyd. Div., Proc. of the Am. Soc. of Civil Eng., vol. 87, no. HY5, pp. 171-194.