Neuman Solution for Unconfined Aquifers

Shlomo P. Neuman (b. 1938), Regents Professor Emeritus of Hydrology and Water Resources at the University of Arizona, derived an analytical solution for unsteady flow to a fully or partially penetrating well in an anisotropic unconfined aquifer with delayed gravity response. The solution assumes a line source for the pumped well and therefore neglects wellbore storage.

The Neuman (1974) solution may be used to determine the hydraulic properties (transmissivity, elastic storage coefficient, specific yield and vertical hydraulic conductivity) of unconfined (water-table or phreatic) aquifers. Analysis involves matching type curves to drawdown data collected during a pumping test.

The delayed yield response described by the Neuman model assumes instantaneous drainage at the water table and exhibits three distinct drawdown segments. Early-time response is controlled by the transmissivity and elastic storage coefficient and is analogous to the response of a confined aquifer. Late-time response is a function of transmissivity and specific yield (drainable porosity). At intermediate time, response is controlled by the aquifer's vertical hydraulic conductivity.

Traditionally, one matches Type A curves to early-time drawdown data and Type B curves to late-time response (Neuman 1975). AQTESOLV provides tools for Type A and Type B visual curve matching plus active type curves for the interpretation of delayed yield in a water-table aquifer.

AQTESOLV uses computational enhancements by Moench (1993, 1996) to calculate type curves for the Neuman solution.

You are not restricted to constant-rate tests with the Neuman solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

Assumptions

• aquifer has infinite areal extent
• aquifer is homogeneous, anisotropic and of uniform thickness
• control well is fully or partially penetrating
• aquifer is unconfined with delayed gravity response
• flow is unsteady
• diameter of a pumping well well is very small so that storage in the well can be neglected

Equations

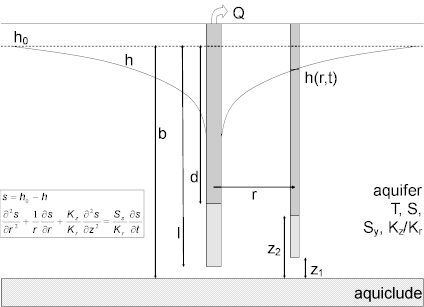
The Neuman (1974) equations for unsteady flow to a partially penetrating well in an unconfined aquifer with delayed gravity response are as follows:

$$s=\frac{Q}{4\pi T}{\int }_0^{\infty }4y{J}_0\left(y\sqrt{}\beta \right)\left[u_0\left(y\right)+\sum _{n=1}^{\infty }{u}_n\left(y\right)\right]\text{d}y\text{(1)}$$ $$\beta =\frac{r^2{K}_z}{b^2{K}_r}\text{(2)}$$ $$\sigma =\frac{S}{S_y}\text{(3)}$$ $$t_s=\frac{Tt}{S{r}^2}\text{(4)}$$ $$s_D=\frac{4\pi T}{Q}s\text{(5)}$$

Drawdown in a piezometer is found using the following equations:

$$u_0\left(y\right)=\frac{\left[1-\text{exp}\left(-t_s\beta \left(y^2-{\gamma }_0^2\right)\right)\right]\text{cosh}\left({\gamma }_0{z}_D\right)}{\left[y^2+\left(1+\sigma \right){\gamma }_0^2-{\left(y^2-{\gamma }_0^2\right)}^2/\sigma \right]\text{cosh}\left({\gamma }_0\right)}·\frac{\text{sinh}\left({\gamma }_0\left(1-d_D\right)\right)-\sinh \left({\gamma }_0\left(1-l_D\right)\right)}{\left(l_D-d_D\right)\text{sinh}\left({\gamma }_0\right)}\text{(6)}$$ $$u_n\left(y\right)=\frac{\left[1-\text{exp}\left(-t_s\beta \left(y^2+{\gamma }_n^2\right)\right)\right]\text{cos}\left({\gamma }_n{z}_D\right)}{\left[y^2-\left(1+\sigma \right){\gamma }_n^2-{\left(y^2+{\gamma }_n^2\right)}^2/\sigma \right]\text{cos}\left({\gamma }_n\right)}·\frac{\text{sin}\left({\gamma }_n\left(1-d_D\right)\right)-\sin \left({\gamma }_n\left(1-l_D\right)\right)}{\left(l_D-d_D\right)\text{sin}\left({\gamma }_n\right)}\text{(7)}$$

The following equations are used to evaluate drawdown in a partially penetrating observation well:

$$u_0\left(y\right)=\frac{\left[1-\text{exp}\left(-t_s\beta \left(y^2-{\gamma }_0^2\right)\right)\right]\left[\text{sinh}\left({\gamma }_0{z}_{\mathrm{2D}}\right)-\text{sinh}\left({\gamma }_0{z}_{\mathrm{1D}}\right)\right]}{\left[y^2+\left(1+\sigma \right){\gamma }_0^2-{\left(y^2-{\gamma }_0^2\right)}^2/\sigma \right]\text{cosh}\left({\gamma }_0\right)}·\frac{\text{sinh}\left({\gamma }_0\left(1-d_D\right)\right)-\sinh \left({\gamma }_0\left(1-l_D\right)\right)}{\left(z_{\mathrm{2D}}-z_{\mathrm{1D}}\right)\left(l_D-d_D\right)\text{sinh}\left({\gamma }_0\right)}\text{(8)}$$ $$u_n\left(y\right)=\frac{\left[1-\text{exp}\left(-t_s\beta \left(y^2+{\gamma }_n^2\right)\right)\right]\left[\text{sin}\left({\gamma }_n{z}_{\mathrm{2D}}\right)-\text{sin}\left({\gamma }_n{z}_{\mathrm{1D}}\right)\right]}{\left[y^2-\left(1+\sigma \right){\gamma }_n^2-{\left(y^2+{\gamma }_n^2\right)}^2/\sigma \right]\text{cos}\left({\gamma }_n\right)}·\frac{\text{sin}\left({\gamma }_n\left(1-d_D\right)\right)-\sin \left({\gamma }_n\left(1-l_D\right)\right)}{\left(z_{\mathrm{2D}}-z_{\mathrm{1D}}\right)\left(l_D-d_D\right)\text{sin}\left({\gamma }_n\right)}\text{(9)}$$

The gamma terms in (6)-(9) are the roots of the following equations:

$$\sigma {\gamma }_0\text{sinh}\left({\gamma }_0\right)-\left(y^2-{\gamma }_0^2\right)\text{cosh}\left({\gamma }_0\right)=0\text{ , }{\gamma }_0^2<y^2\text{(10)}$$ $$\sigma {\gamma }_n\text{sin}\left({\gamma }_n\right)+\left(y^2+{\gamma }_n^2\right)\text{cos}\left({\gamma }_n\right)=0\text{(11)}$$ $$\left(2n-1\right)\left(\pi /2\right)<{\gamma }_n<n\pi \text{,}n\ge 1$$

where

• $b$ is aquifer thickness [L]
• $d_D$ is dimensionless depth to top of pumping well screen (d/b)
• $J_0$ is Bessel function of first kind, zero order
• $K_r$ is the radial (horizontal) hydraulic conductivity [L/T]
• $K_z$ is the vertical hydraulic conductivity [L/T]
• $l_D$ is dimensionless depth to bottom of pumping well screen (l/b)
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $s$ is drawdown [L]
• $S$ is elastic storage coefficient [dimensionless]
• $S_y$ is specific yield [dimensionless]
• $t_s$ is dimensionless time with respect to S
• $t$ is elapsed time since start of pumping [T]
• $T$ is transmissivity [L²/T]
• $y$ is a variable of integration
• $z_D$ is dimensionless elevation of piezometer opening above base of aquifer (z/b)
• $z_{\mathrm{1D}}$ is dimensionless elevation of bottom of observation well screen above base of aquifer (z₁/b)
• $z_{\mathrm{2D}}$ is dimensionless elevation of top of observation well screen above base of aquifer (z₂/b)

The foregoing equations developed by Neuman (1974) can be difficult to evaluate in practice; therefore, AQTESOLV incorporates more efficient numerical methods developed by Moench (1993, 1996) for the computation of the Neuman solution.

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• aquifer saturated thickness
• partial penetration depths (optional)

Solution Options

• variable pumping rates
• multiple pumping wells
• multiple observation wells
• partially penetrating pumping and observation wells
• boundaries

Estimated Parameters

• $T$ (transmissivity)
• $S$ (elastic storage coefficient)
• $S_y$ (specific yield)
• $\beta$ or $K_z/K_r$ (hydraulic conductivity anisotropy ratio)

AQTESOLV displays $\beta$ for tests with a single observation well or $K_z/K_r$ for multiple observation wells.

Curve Matching Tips

• Use the Cooper and Jacob (1946) solution to obtain preliminary estimates of aquifer properties. Determine T by matching a straight line to late-time data. If the wells are fully penetrating, you also may estimate Sy from the late-time match. Obtain an approximate estimate S from early-time data.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $\beta$ and $K_z/K_r$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

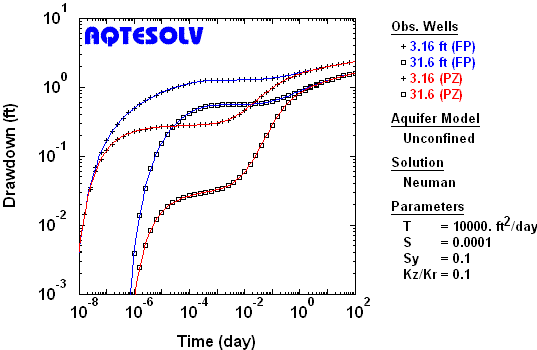
Benchmark

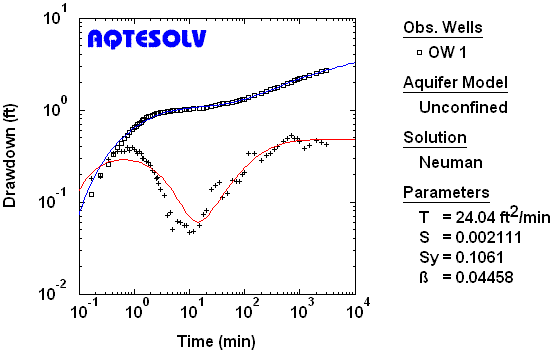
Example

References

Neuman, S.P., 1974. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response, Water Resources Research, vol. 10, no. 2, pp. 303-312.